Los veranos de clima continental moderado (o mediterráneo continentalizado) pueden ser muy cálidos y secos donde sólo las especies más rústicas tienen posibilidades de prosperar. Así que si queremos ampliar el abanico de plantas y árboles productores de comida, es necesario disponer de agua para el verano, sobre todo para establecer el bosque de alimentos. Más tarde, cuando todo esté más crecido y haya árboles que provean de sombra al conjunto, cortavientos que frenen el aire, etc. casi seguro que se forma un pequeño microclima que mantiene la humedad y con menos agua todo es posible. Pero para empezar, se necesita agua y en mi terreno no puedo contar con más agua que la de la lluvia, pues no hay posibilidad de regadío, ni hay manantiales. Está en un alto y los manantiales en esta zona están todos en las zonas bajas del valle.
Sin embargo, creo que he encontrado una buena solución al reto de cosechar agua para el verano. Geoff Lawton hace diseños para fincas enormes y en esta mi finca, que es de 14 celemines y encima algo dispersos, si hago un dique de contención para retener el agua de lluvia en un estanque, me cargo la mitad del terreno disponible. Dándole vueltas he llegado a este diseño en el que se unen varias cosas: ocupa poco espacio, los materiales están disponibles, puedo hacer tantos como y cuando necesite y es relativamente barato. Y voy a poner a disposición del que lo quiera copiar para su uso particular todas las instrucciones en esta entrada y la que será la siguiente. El diseño del Modelo A es mío y la idea fue mejorada con el Modelo B por mi amigo Lurgorri Abeledo.
Sin embargo, creo que he encontrado una buena solución al reto de cosechar agua para el verano. Geoff Lawton hace diseños para fincas enormes y en esta mi finca, que es de 14 celemines y encima algo dispersos, si hago un dique de contención para retener el agua de lluvia en un estanque, me cargo la mitad del terreno disponible. Dándole vueltas he llegado a este diseño en el que se unen varias cosas: ocupa poco espacio, los materiales están disponibles, puedo hacer tantos como y cuando necesite y es relativamente barato. Y voy a poner a disposición del que lo quiera copiar para su uso particular todas las instrucciones en esta entrada y la que será la siguiente. El diseño del Modelo A es mío y la idea fue mejorada con el Modelo B por mi amigo Lurgorri Abeledo.
 |
| Así más o menos deben ser las bandejas que pretendo hacer para recoger agua en medio del campo |
Es bastante sencillo en España encontrar depósitos de 1000 L. Se encuentran de segunda mando en Internet a un precio asequible, barato, diría yo, para el beneficio que nos pueden proporcionar a lo largo de muchos años. El resto de los materiales han sido comprados en una de las tiendas de una multinacional de bricolaje y los mostraré con detalle en la segunda parte de esta entrada.
Lo habitual es recoger el agua de un tejado y canalizarla hasta el depósito pero en la finca no hay ningún tejadillo que pudiera servir para tal fin. Mi idea es diseminarlos por aquí y por allá, expandiendo a partir de ellos los cultivos. Y para eso lo mejor es que lleven una bandeja con ellos, copiando la bandeja la función captadora del tejado.
La primera duda que aparece es cuán grande ha de ser esa bandeja y eso, claro está, dependerá de las precipitaciones anuales que tengamos. Hay que volver a esta entrada, donde calculaba el agua que podría en teoría recoger el pedazo principal de mi finquita, y lo aplicamos, al revés, al agua que queremos recoger. Como no os quiero aburrir con los cálculos, los dejo para la parte final de la entrada, por si alguien los quiere usar para adaptarlos a sus circunstancias. Yo los he aplicado y he visto que necesito una plancha de 0,98*2,07 para el Modelo A o dos planchas de 0,98*1,04 para el modelo B con unas precipitaciones de 550 mm anuales que son las que tengo. Si quieres copiar este diseño, busca las precipitaciones en mm en tu zona, mira cómo son el depósito y la plancha que tienes e introdúcete en el desarrollo, cambiando tus parámetros. Pero por si definitivamente aborreces las matemáticas, lo he calculado partiendo del mismo tipo de depósito para algunas de las diferentes precipitaciones de España.
La primera duda que aparece es cuán grande ha de ser esa bandeja y eso, claro está, dependerá de las precipitaciones anuales que tengamos. Hay que volver a esta entrada, donde calculaba el agua que podría en teoría recoger el pedazo principal de mi finquita, y lo aplicamos, al revés, al agua que queremos recoger. Como no os quiero aburrir con los cálculos, los dejo para la parte final de la entrada, por si alguien los quiere usar para adaptarlos a sus circunstancias. Yo los he aplicado y he visto que necesito una plancha de 0,98*2,07 para el Modelo A o dos planchas de 0,98*1,04 para el modelo B con unas precipitaciones de 550 mm anuales que son las que tengo. Si quieres copiar este diseño, busca las precipitaciones en mm en tu zona, mira cómo son el depósito y la plancha que tienes e introdúcete en el desarrollo, cambiando tus parámetros. Pero por si definitivamente aborreces las matemáticas, lo he calculado partiendo del mismo tipo de depósito para algunas de las diferentes precipitaciones de España.
 |
| Precipitaciones anuales medias en España y Portugal |
A continuación pongo las tablas por si queréis hacer algo parecido en vuestros terrenos. El largo que tiene que ser la plancha está en la fila "LADO plancha (hipotenusa)".
 |
| Tabla de medidas de la bandeja de una sola hoja (Modelo A) |
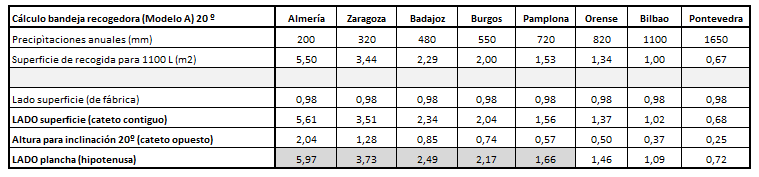 |
| Y las medidas para la bandeja de una sola hoja tomando un ángulo de inclinación de 20º |
El modelo A es más fácil de construir: una plancha, 4 soportes de fijación y algún tipo de canaleta o canalón que recoja ese agua y la lleve al depósito, pero tiene un problema para climas muy secos: la plancha es excesivamente larga si queremos que proporcione la suficiente superficie de recogida cuando llueve poco. Es excesiva porque para empezar dónde podremos encontrar una plancha tan larga, luego tenemos el problema de fijarla adecuadamente para que con tanto voladizo no se caiga y finalmente, si somos tozudos y la fijamos perfectamente al depósito, aparece el riesgo de que con vientos fuertes forme una gran vela que haga que se lleve el depósito cuando está vacío o que rompa la plancha, si no se puede llevar el depósito a rastras.
He marcado en gris los valores que yo no contemplo como viables de una manera intuitiva, pues habría que calcular la fuerza del viento, la resistencia de los materiales, etc. y ahí ya no llego. Además, aunque me he divertido bastante calculando cuáles son las dimensiones más adecuadas de la bandeja para mis precipitaciones, tampoco se trata de mandar un cohete a la Luna, es solo un depósito en medio de un campo al que se le pide que recoja todo el agua que pueda.
El modelo B viene a mejorar las limitaciones de la bandeja anterior. Al estar la superficie de recogida dividida en dos planchas, al repartirse entre ellas el voladizo, te permite que la superficie sea mayor. Es un poco más laboriosa de fabricar, pero solo un poco.
 |
| Tabla de medidas cada una de las hojas de la bandeja en forma de libro (Modelo B) |
 |
| Y las medidas de cada una de las hojas tomando un ángulo de inclinación de 20º (Modelo B) |
Pues esto es todo. Me gusta mucho la filosofía de Open Source en la que ponen a disposición de cualquiera que tenga conexión a Internet planos y cálculos para que cada uno pueda hacerse sus propias máquinas o artilugios, y a ella me uno con esta pequeña aportación que creo que a mí me va a ser muy útil. Es un prototipo y como tal es absolutamente mejorable. Si alguien quiere compartir su mejora o los defectos que pueda haber, soy toda oídos.
La siguiente entrada será más práctica, explicando cómo lo hemos hecho. Aquí os dejo un adelanto:
 |
| ¡Ya está casi! |
CUIDADO: Cálculos matemáticos, sòlo para valientes
Mis precipitaciones anuales en Burgos son de 550 mm (0,55 m) y en Bilbao de 1100 mm (1,1 m) y quiero llenar un depósito de 1000 L (1 m3). Ya que la precipitación anual es una media, previendo que algunos años puedan ser más secos, voy a tomar como objetivo de recogida aproximadamente 1100 L (1100 L = 1,1 m3).
Vamos a calcular el Modelo A que es más fácil y el siguiente cálculo sirve para las precipitaciones anuales de Burgos.
Esta es la fórmula que sirve para calcular la superficie de recogida necesaria en cualquier zona del mundo:
Mis precipitaciones anuales en Burgos son de 550 mm (0,55 m) y en Bilbao de 1100 mm (1,1 m) y quiero llenar un depósito de 1000 L (1 m3). Ya que la precipitación anual es una media, previendo que algunos años puedan ser más secos, voy a tomar como objetivo de recogida aproximadamente 1100 L (1100 L = 1,1 m3).
Vamos a calcular el Modelo A que es más fácil y el siguiente cálculo sirve para las precipitaciones anuales de Burgos.
Esta es la fórmula que sirve para calcular la superficie de recogida necesaria en cualquier zona del mundo:
Precipitaciones anuales (m) x Superficie de recogida (m2) = Agua recogida (m3)
Y para el caso de Burgos:
Precipitaciones anuales = 0,55 m
Superficie de recogida = ?
Agua objetivo = 1,1 m3
Sustituyendo en la fórmula anterior:
0,55 x Superficie de recogida = 1,1 m3
Superficie de recogida = 1,1 / 0,55 = 2 m2
Para unas precipitaciones de 550 mm necesitamos 2 m2 de superficie recogida y con ese dato, usando la trigonometría, el teorema de Pitágoras y la fórmula del área del rectángulo, vamos a las dimensiones de la plancha que va a desaguar en el canalón de recogida que, a su vez, desagua en el depósito.
Si nos colocamos justo encima del depósito y miramos para abajo, veríamos el rectángulo que forma/n la/s plancha/s que es igual a la superficie de recogida. En el dibujo de arriba "S"
Esta es la formula de la superficie del rectángulo:
LADO x lado = Superficie
En mi caso, uno de los lados lo da la propia plancha que he comprado, ella es así, con lo que ya tenemos un dato. Entonces:
LADO = ?
Lado = 0,98 m (de fábrica)
Superficie = 2 m2
Sustituyendo en la fórmula anterior:
LADO x 0,98 = 2 m2
LADO x 0,98 =2
LADO = 2/0,98 = 2,04 m
Ya sabemos que nuestra superficie de recogida es de 0,98 m x 2,04 m.
Para que el agua caiga por gravedad en el canalón de recogida y no se desparrame por los lados hacia el suelo y no hacia el depósito, que es donde la queremos conducir, vamos a darle una inclinación de 10º a las planchas. No es mucho pero tampoco queremos que levante más de la cuenta y forme demasiada vela. Además, cuanto más ángulo más larga será la plancha que vamos a necesitar.
Aquí es donde podemos echar mano de la trigonometría. Para explicaciones al respecto mirad esta página. Conocemos el "cateto contiguo" (2,04) y sabemos que:

Entonces en este caso para 10º de inclinación:
siendo:
c = hipotenusa
a = cateto contiguo
b = cateto opuesto
Para que el agua caiga por gravedad en el canalón de recogida y no se desparrame por los lados hacia el suelo y no hacia el depósito, que es donde la queremos conducir, vamos a darle una inclinación de 10º a las planchas. No es mucho pero tampoco queremos que levante más de la cuenta y forme demasiada vela. Además, cuanto más ángulo más larga será la plancha que vamos a necesitar.
Aquí es donde podemos echar mano de la trigonometría. Para explicaciones al respecto mirad esta página. Conocemos el "cateto contiguo" (2,04) y sabemos que:
cos α = Cateto contiguo / Hipotenusa
Entonces en este caso para 10º de inclinación:
Cos 10º = Cateto contiguo / Hipotenusa = 0.984807753012208
Hipotenusa = 2,04 / 0.984807753012208 = 2,07 m
La hipotenusa es la longitud desconocida de la plancha, por tanto, para Burgos es necesaria una plancha de 0,98 x 2,07.
Y como ejemplo, por si alguien piensa que 10º es poco y quiere darle 30º, obtendrá que la plancha a utilizar tiene que ser más larga:
Cos 30º = Cateto contiguo / Hipotenusa = 0.8660254037844387
Hipotenusa = 2,04 / 0.8660254037844387 = 2,35 m
Para calcular el cateto opuesto que corresponde a la altura que tenemos que darle al soporte más extremo de la plancha, bastaría con calcular el seno de 10º pero ya que estoy desempolvando las matemáticas que aprendí hace muchos años, vamos a aplicar el teorema del amigo Pitágoras, el teorema que decía aquello de:
En todo triángulo rectángulo el cuadrado de la hipotenusa es igual
a la suma de los cuadrados de los catetos
y en lenguaje matemático
c2 = a2 + b2
siendo:
c = hipotenusa
a = cateto contiguo
b = cateto opuesto
Y en este caso:
c =2,07
a = 2,04
b =?
Sustituyendo en la fórmula anterior:
2,07 x 2,07 = 2,4 x 2,04 + b2
b2 = 2,07 x 2,07 - 2,4 x 2,04
b2 = 2,07 x 2,07 - 2,4 x 2,04
b = 0,36 m
Para que luego digan que las matemáticas no sirven para nada...

























